I’ve detailed on this blog all of our troubles with various sensor solutions. Historically we’ve used a two-part system: an accelerometer plus an infrared absolute reference. But with polycarbonate reflections and scaling issues as they are, we’ve long sought a replacement.
I tried a magnetometer early on, as it seemed like the perfect solution. What other reference do we need than magnetic North? But initial testing led me to write it off.
Initial magnetometer test data
The data above was dumped from Hit ‘N Spin running at full speed. I was attempting to do a soft/hard iron calibration on it, so I expected to see some kind of ellipse. What I actually got was garbage enough that I assumed something else was going on.
I used an off-the-shelf commercial IIC magnetometer sensor. I thought ahead that the high G forces could disrupt a MEMS sensor, so I made sure to grab a hall-effect based one. But When I looked back at the datasheet after this test, I noticed one number was missing: maximum rotation speed.
In fact, that number was missing from lots of magnetometer datasheets. Now, it’s probably safe to assume that 1500RPM operation is not something the typical magnetometer designer has in mind. So it’s probably safe to assume that the averaging periods in the typical magnetometer impose a maximum speed well below what I need.
I asked some knowledgeable folks, I googled and googled, and then finally gave up. It wasn’t to be.
Or so I thought…
While moping after my machine-vision based idea didn’t pan out, I had the thought: instead of finding a sensor that works despite my tough environment, is there a sensor that works because of my tough environment? That was the inspiration needed, and it brings us to Faraday’s law.
The Physics
This section is pretty mathy, and more for people with some background already. TLDR for those who want to skip ahead: spinning a coil on earth makes a voltage that we can get the magnetic heading from.
For a coil of wire of N turns, each with the same magnetic flux $\Phi_B$, the electromotive force $\varepsilon$ across the coil is:
$$\varepsilon=-N\frac{d\Phi_B}{dt}$$
This is basically saying that magnetic fields cause a voltage ($\varepsilon$) to appear across coils of wire. Definitions out of the way, lets explain a little bit. The earth has a magnetic field, that is present everywhere on the surface. It has varying strength and direction from place to place, but it can be roughly approximated as a uniform field pointed north of value $B_E=50\mu T$
When you place a loop of wire in a magnetic field, some “amount” of that field passes through the loop. This “amount” has a name: magnetic flux $\Phi$. Now, if you make the loop bigger, more field passes through the loop, which increases flux. Of course, increasing the field strength also increases flux. In our scenario we know that the field strength is uniform, so we can use a simple definition of flux:
$$\Phi=AB_E$$
Where A is the area of the coil. Now, lets expand on this scenario a little bit. Say the coil happens to be in a meltybrain. This means it is spinning, so the field strength experienced by the coil is no longer constant. It will vary from $-B_E$ to $+B_E$ as it points from north to south and back again. We can model the field like this:
$$B_R=B_E\sin(\theta(t))$$
Where $\theta$ is the direction we’re facing in radians. Note that I added a (t) here, as we must consider that $\theta$ varies with time in the following steps. Lets plug that back into Faraday’s law.
$$\varepsilon=-NAB_E\sin(\theta (t))\frac{d}{dt}$$
Sorry, the $\frac{d}{dt}$ here does mean calculus, but thankfully it’s an easy derivative. Just don’t forget chain rule, which pulls out the $\theta(t)\frac{d}{dt}$ as $\omega$, or rotation speed.
$$\varepsilon=-NAB_E\omega\cos(\theta)$$
This tells us that if you put a coil of wire in a meltybrain, it will produce a voltage that is proportional to:
Coil geometry (area, number of turns)
Field strength
Rotation speed
Heading angle
That’s right folks, math says we can measure a voltage and get a heading angle from it! It’s exactly the sensor we’re looking for. Let’s plug in some expected numbers and see if it’s sane:
$$\varepsilon=-(3000)(0.025m*0.038m)(0.00005T)(157rad/s)\cos(\theta)$$
$$\varepsilon=-0.022\cos(\theta)$$
Summing up, our thought experiment coil will give us a signal with a 22mV amplitude. That is absolutely enough to work with given some amplification.
This isn’t a new concept
In chatting with people about this, I learned that this type of magnetometer is actually quite old, known as a rotating coil magnetometer. But creating one is typically mechanically complex, because you would typically need an interface between a spinning bit and a stationary bit.
But for a meltybrain, it’s absolutely perfect.
The Electronics
Now that we know to expect a signal in the ~10mV range, lets talk some analog engineering. It’ll be much easier to work with it in the 1V range, so lets shoot for 100X amplification.
What’s So Hard About Measuring 22mV?
Well, to start with…
Source Impedance
My latest coil produces a voltage of about 4mV at 18Hz rotation rate. It has a total resistance of 500Ω. So how much current can we pull from it before IR drop cancels out our signal?
$$\frac{V}{R}=I$$
$$\frac{0.004}{500}=8\mu A$$
And it’s linear, so if we pull even half that much we lose half of our signal. It’s safe to say that the coil has the drive strength of a wet noodle.
So as part of our analog design, we need an input buffer. This is device that will drive a copy of whatever signal it’s receiving, except:
It pulls almost no current from the input
It can drive a lot of current to the output
Noise
Every sensor picks up noise, we’re no exception. Our coil will pick up and amplify any magnetic field that happens across it, and incidental Noise needs to be dealt with via a filter.
This is a case where our sensor has an advantageous quality: our “signal of interest” is at a frequency of ~20Hz depending on speed. That's practically DC, so it’s unlikely we’ll pick up something with a similar frequency.
But what about your circuit board/battery currents? A savvy reader might ask. Yes, the nearby LiPO battery will generate a significant DC magnetic field from driving the motors. But crucially, that field will be mechanically stationary with respect to the coil. Faraday’s law says it won’t get picked up at all!
To sum up, we need a low-pass filter.
Above shows my LTSpice design for a sallen-key second-order low-pass filter, configured for unity gain and a 500Hz cutoff frequency. This filter will pass, undisturbed, any signal below 500Hz. But above that, it will attenuate the signal by 20dB per decade. So a 5kHz signal is reduced by 10X, a 50kHz signal by 100X, and so on. The solid green line in the bode plot graph above shows this in action.
Based on my testing and analysis, this filter should be enough to quash most noise problems we might experience.
Filter Phase Shift
Of course, everything is a trade off, and that strong filter introduces a slight wrinkle. see that dashed line in the graph above? That is the phase shift that the filter introduces to the signal. This means that our forward reference will be off a certain amount, increasing with speed. According to this simulation, it should only get as bad as ~10º, so it’s a known error I’m going to accept.
Analog wrap up
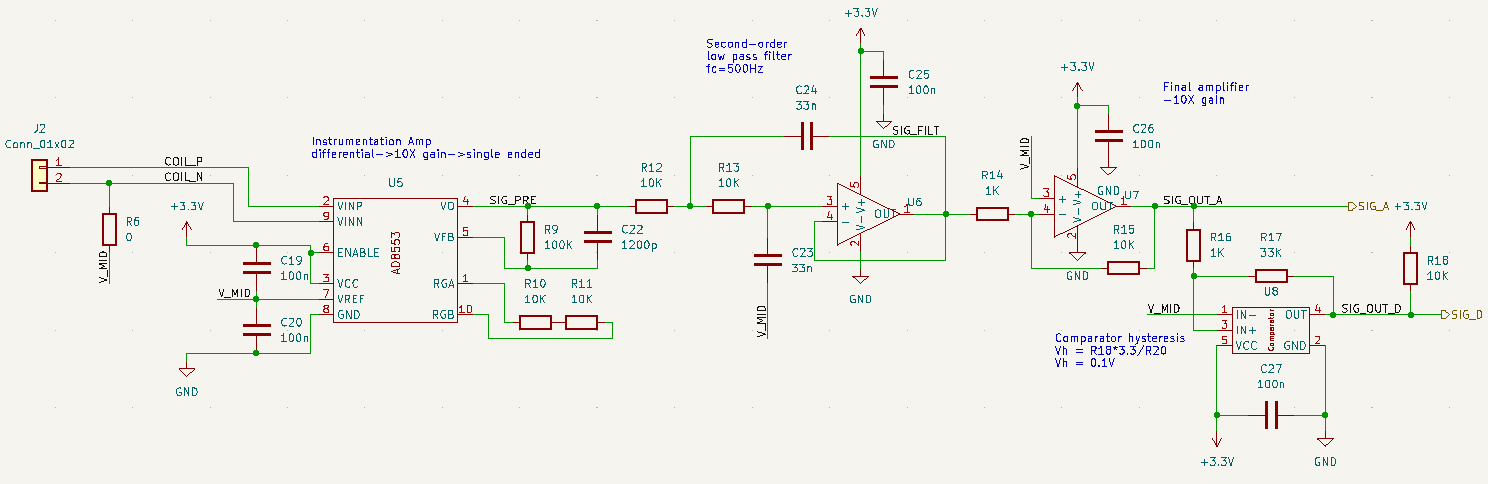
After a significant amount of test and iteration, here’s the schematic I ended up with. The image resolution is kind of poor, but you can find a pdf copy here.
The final analog front-end schematic.
The AD8553 is an instrumentation amplifier, which is a type of amplifier specially designed for measuring weak differential signals. It’s perfect for an input buffer, and it provides a 10X gain to boot.
Then the pre-amplified signal is filtered by the circuit we saw earlier. And finally, a simple -10X gain inverting amplifier is used to take us to the total 100X gain.
The multi-stage nature of this design meant I had to look for op-amps with low input offset voltage, else this error term would get amplified too and cause problems.
There’s also a comparator in this circuit, I’ll get to that in a bit. First my oscilloscope capture:
Test data taken from the rig pictured at the top. Yellow is the analog signal, blue the comparator output.
There is a clear 0.8V pk-pk signal present in the view. There is also a particular noise component, but further testing indicated that it was introduced by the co-located brushed motor in my test rig. So I don’t expect it to be present in the arena.
Though even if the noise were to stay, this signal is good enough to work with directly.
The Code
And by code, I mean math. Hah! Bet you thought we left that in the physics section!
We have to figure out how our code can turn our measured voltage into an angle. There are two methods I’ve identified, though skip ahead to #2 if you’re just interested in replicating what we compete with. Method #1 is detailed here for posterity.
Method #1: Direct Conversion
The obvious route is to run the measurement through an equation to get a heading. Let’s start by re-arranging the EMF equation we derived earlier.
$$\varepsilon=-NAB_E\omega\cos(\theta)$$
$$\theta=\cos^{-1}(\frac{-\varepsilon}{NAB_E\omega})$$
At this point I’m going to swap the cosine with a sine to make it easier to talk about. This introduces a 90º phase shift in the result, but as I will discuss later it doesn’t have any practical effect.
$$\theta=\sin^{-1}(\frac{-\varepsilon}{NAB_E\omega})$$
We do have one extra unknown here, and that is $\omega$. We could measure $\omega$ directly with an accelerometer, but part of the draw of this system is we shouldn’t need an accelerometer. So there’s a better idea: autocalibrate!
We can reasonably assume that each peak and trough will be roughly the same height as the previous one. The faster we’re accelerating the more that’s not true, but it’s likely a good enough assumption for it to help. In this case, we can have our software watch for peaks and troughs. Every time we hit one, we note the value. At peaks and troughs $\sin(\theta)$ must be 1 or -1, so we can be sure the absolute value of the measured signal is equal to everything else:
$$abs(\varepsilon_{peak})=NAB_E\omega=V_{cal}$$
With that value saved, we have an easier equation.
$$\theta=\sin^{-1}(\frac{V_{meas}}{V_{cal}})$$
This simple equation belies some complexity however. A typical inverse sine isn’t actually a true “reverse sine”. This is because a true reverse sine would give two results for every input. For example, we know:
$$\sin(\frac{\pi}{4})=\sin(\frac{3\pi}{4})=\frac{1}{\sqrt{2}}$$
So if you were to try to evaluate $\sin^{-1}(\frac{1}{\sqrt{2}})$, $\frac{\pi}{4}$ and $\frac{3\pi}{4}$ could both be the result.
We need some more information to figure out which result is correct, and we can get that by tracking previous measurements. Given a set of two angles with equivalent sines, math says that the slope of the sine wave at those two angles should be opposite signs. So if we track whether the measurements are increasing or decreasing, we can figure out which result is correct. And now we have our heading!
A note on precision
As the signal begins to approach a peak or a trough, the volts per degree will approach zero. Put another way, the closer we are to the peak or a trough the less precisely our ADC will be able to resolve our heading measurement. For a real system, there will be two ranges of angles in which noise will make your heading measurement essentially a random value in that range.
Method #2: Zero Crossing Extrapolation
This is the method that we are going to compete with, because it is much simpler than direct conversion. It could be construed as less accurate, but it doesn’t suffer from the precision issues noted above so it’s a toss up on which gives a better heading fix.
The first step is to feed the amplified and filtered signal to a comparator referencing the sine wave’s midpoint. Remember that blue line on the scope plot? That’s the comparator. You will need to add some hysteresis to the comparator circuit to account for noise (and I clearly need more in the plot above). Feed the comparator output directly to a GPIO pin.
Have your microcontroller trigger an interrupt on every GPIO state change. Inside the interrupt, note a timer count of when we triggered, and what value the GPIO is. If the GPIO is high, then we know that our signal just crossed the zero line on a positive slope. We will call this our “North” direction. I don’t actually know if it’s North, I haven’t done the math, but it doesn’t matter.
Similarly, If the GPIO is low, our signal just crossed the zero line on a negative slope. This is “South”.
All other values of our sine wave are irrelevant, we only care about zero crossings. This provides a nice benefit of ignoring any changes in signal amplitude, unlike the direct conversion method.
Now that we have a time fix on our previous zero crossings, we can extrapolate forward to figure out where we are now. This calls up the exact same math I employed in previous posts, halo pt. 6 and halo pt. 7. Except instead of points spaced 360º apart, we have points spaced 180º apart, making our extrapolation twice as accurate. Copying the equation from part 6:
$$\theta(t) = \theta_{k-1}+\frac{t-t_{k-1}}{t_k-t_{k-1}}(\theta_k-\theta_{k-1})$$
The numbers we plug in here depend on which edge we saw last, because the values of $\theta_k$ and $\theta_{k-1}$ will change. We will recognize rising edge to be $\theta_r=0$ and falling edge to be $\theta_f=180$.
First, the "last edge was rising" equation:
$$\theta_{rose}(t)=180\frac{t-t_f}{t_r-t_f}-180$$
Finally, the "last edge was falling" equation:
$$\theta_{fell}(t)=180\frac{t-t_r}{t_f-t_r}$$
These two equations are the only work your MCU needs to do to calculate heading, given that you have an interrupt that is recording the edge time.
It will be more inaccurate the more the robot is accelerating and the further since the last zero crossing, but you can adapt the math from part 7 to improve it if needed.
Method #2 presents a substantially simpler digital design compared to Method #1. Requiring an interrupt instead of an ADC, and with a much simpler math equation, it should be less taxing on your processor. This is why it is our method of choice for our next generation of robots.
Got a wobble problem?
I encountered an issue with my test rig, where the tracking was consistently off. After some experimentation, I captured this plot:
The output of a wobbly system
Essentially my test rig was wobbly in a consistent way, where the first 180º of travel took less time than the last 180º of travel. This caused the duty cycle of my digital signal to be off, which created a consistent error term.
I don’t expect this wobble to persist once I mount it to an actual robot. But if it ever does persist, you can drop to only tracking one edge per revolution instead of both, ala the beacon tracking algorithm. This is less accurate, but immune to wobble and still pretty good.
Let’s Talk About Phase Shift
Phase shift in the context of this system basically refers to “where does the robot think North is as opposed to where it actually is.”
This system needs to be an absolute reference, but not a correct one. So as long as where it thinks North is stays locked in a particular direction, it doesn’t practically matter if “North” is actually East. And regardless, you can’t control what direction the arena will be facing, so you’ll likely need to apply a constant “North” adjustment anyways to make “forward” a sensible direction. If you have an adjustment dial, then “North” being North matters even less!
This allows us to make many design simplifications throughout.
The one place where phase shift is bad is if the phase shift is not constant, like in the case of the low pass filter noted above. A varying phase shift breaks the “absolute” quality of this sensor, so any such effects must be minimized.